Naissance du projet PPPE

À l’université de Pau et des Pays de l’Adour (UPPA), en partenariat avec le Lycée Louis Barthou de Pau, le PPPE propose deux parcours de licence, un en licence MIASH (Mathématiques et Informatique Appliquées aux Sciences Humaines et Sociales) et l’autre en licence Lettres, ayant pour but une préparation progressive au métier de professeur des écoles. Après l’obtention d’une telle licence, l’étudiant pourra intégrer un master MEEF pour passer ensuite le concours de professeur en école primaire.

Voici comment est né ce parcours PPPE.

En 2021, il y a eu tout d’abord un appel à projet national, auquel ont répondu le Président de l’UPPA et le Proviseur du Lycée Barthou à Pau. L’équipe pédagogique de l’UPPA a eu connaissance de cette réponse et, avec les moyens du bord, trois enseignants, concernés par la licence Miash, ont monté le projet : Laurent Lévi (responsable licence Miash), Marc Dambrine & Guy Vallet.

En parallèle, Cécile Rochelois, Bérengère Moricheau-Airaud et Julie Gallego montaient le projet pour la licence de Lettres puisque c’est un double PPPE : Miashs et Lettres.

Au Lycée Barthou, Marc Lalaude et Arnaud Rochelois ont été les responsables de l’organisation, respectivement pour les Miashs et les Lettres.

Naissance, au sein du PPPE, du parcours « contes mathématiques »

Il s’agit d’un appel à manifestation d’intérêt « Qualité et Innovations Pédagogiques » avec plus ou moins la même équipe, financé pour 2023/24.Les co-initiateurs du projet sont Marc Lalaude, Guy Vallet, Laurent Lévi.

Contenu & motivation

L’idée : il s’agit, à l’instar d’un petit nombre de livres “pilote”, de donner à voir, à entendre, un imaginaire pensé pour pouvoir être réinvesti indirectement dans l’apprentissage des mathématiques

Ce projet est pilote pour l’année 2023-2024 et nous souhaitons qu’il soit reconduit et qu’en trois années il prenne une forme finalisée, ayant fait ses preuves, et digne de devenir une U.E. à part entière. ##

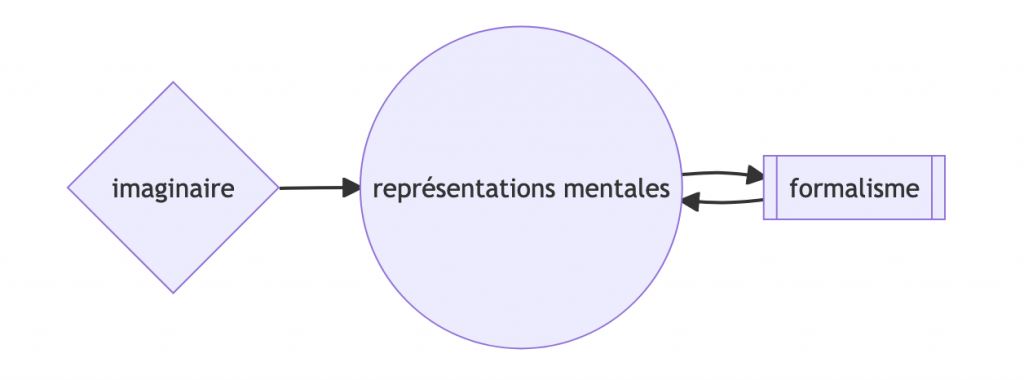
-> Dans ce projet il ne s’agit pas de réaliser des illustrations jolies pour “habiller” des exercices de maths : il s’agit de créer des univers imaginaires dont les éléments peuvent être réinvestis : un élève qui aborde les maths en CM2, en 6e, au lycée, dans le supérieur, peut s’appuyer sur des représentations mentales riches, s’il en a, pour développer l’idée qu’il se fait des objets mathématiques. Ensuite, par un chemin d’allers-retours entre cette intuition (ces représentations mentales) et le formalisme rigoureux, il aura un bon outil pour comprendre. C’est la thèse que, par exemple, développe David Bessis dans son ouvrage Mathematica.

Exemple

Imaginons les deux idées suivantes :

	idées imaginaires	idées mathématiques
éléphant	– Elmer – contes 1000 & 1 nuit – Dumbo – Charlemagne	– compter les pas – volumes d’eau – personnifer variable mémoire – géométrie
tour	– Tour Eiffel – Tour de Pise – tour des échecs – tour de Babel	– dénombrer escaliers/étages – nombres relatifs (sous-sols) – additions à trous – algo

Explications détaillées :

• Elmer, contes 1000 & 1 nuit, Dumbo font référence à des histoires connues dont on peut s’inspirer ;
• Charlemagne permet un lien historique (classe de 5e) avec l’éléphant albinos que le sultan Haroun-Al-Rachid a offert à Charlemagne ;
• “compter ses pas” permet de travailler la multiplication par 4, par exemple sur un parcours avec des cases avancer d’une case revient pour l’éléphant à effectuer 4 pas ; ceci peut être mimer par deux enfants (l’un appuie ses mains sur les épaules de l’autre) faisant l’éléphant sur un parcours tracé à la craie sur le sol ;
• “volumes d’eau” fait référence à la capacité qu’a l’éléphant d’aspirer avec sa trompe et permet des problèmes de transvasement et de volume, adaptés à la classe où l’on travaille ;
• “personnifier variable mémoire” signifie que si on initie les enfants aux algorithmes, le concept de “variable” peut être personnifié par l’élphant, en rapport avec la qualité de grande mémoire qu’on prête à cet animal ;
• “géométrie” suppose l’idée d’un pavage avec des polygones simples, et qui représenterait un éléphant ;
• “dénombrer escaliers/étages” : s’il faut \(n=10\) marches d’un étage à l’autre et si mon petit robot a l’autonomie de sauter 33 marches, jusqu’à quel étage arrive-t-il (on peut décliner d’autres valeurs de \(n\)) ;
• “nombres relarifs” car typiquement l’ascenseur est le lieu où l’on peut se fair des représentations d’une opération comme \(2-5=-3\) ;
• additions à trous : pour aller de l’étage 57 à l’étage 72 combien d’étages dois-je franchir ? (prémisse de la soustraction) ;
• algo : par exemple, un petit diable regarde le nombre d’étage \(n=5\) et le transforme pendant la nuit en \(2\times x-4\), observer l’évolution de \(n\) sur plusieurs nuits…
• on peut aussi imaginer encore et encore, par exemple le poids d’un éléphant qui porte un oiseau, deux oiseaux, trois oiseaux (notion de négligeable)

Réalisations

Avec les 5 étudiants de L3 PPPE ayant choisi l’option facultative “contes mathématiques”, nous projetons :

• la réalisation de 5 petits albums ;
• la réalisation d’exercices de maths prototypes s’appuyant sur l’imaginaire de chacun de ces 5 albums ;
• création d’une capsule vidéo.