L’origami mathématique est une discipline récente qui prend véritablement son envol au début des années 1990. On trouvera une présentation de cette discipline dans la conférence sur les origamis transformables, donnée la première fois dans le cadre d’une conférence aux journées nationales de l’association des professeur de mathématiques de l’enseignement public (APMEP) en octobre 2018 à Bordeaux
Pour les lecteurs curieux au niveau mathématique, je renvoie au livre de Joseph O’Rourke

Dans la suite, on donne un ensemble d’origamis que l’on peut réaliser dans les classes.
La double hélice d’ADN
C’est un des pliages que je préfère et qui peut être réalisé par les plus petits. Il suffit de prendre une feuille a4 et de la plier en deux afin d’obtenir une bande qui va constituer la feuille que l’on va plier. Voila les étapes du pliage:

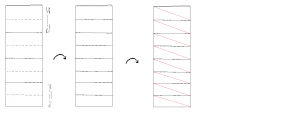
Je vous conseille de faire les pliages des diagonales de chaque rectangle en utilisant une règle et un stylo et de bien appuyer afin de bien marquer l’endroit du pli. Les trais noirs sont des plis vallées et les plis rouges des plis montagnes (vous pouvez bien entendu faire le contraire !).
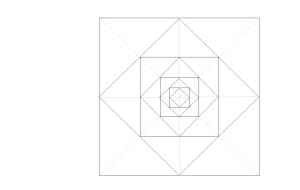
C’est l’angle que fait cette diagonale qui va induire la vitesse d’enroulement de votre hélice. Cet angle est lui contrôlé par la première phase du pliage, c’est à dire le nombre de plis horizontaux que vous aurez fait !
Pour des élèves de collèges ou de lycées on peut se poser la question de l’enroulement « limite » que l’on peut obtenir ainsi…..Cette activité est détaillée dans le livre de Thomas Hull « Project Origami – Activities for exploring mathematics » publié aux éditions CRC Press (activity 5 dans le livre).
Vous trouverez une vidéo expliquant ce pliage étapes par étapes ici:
Origami « La boite à secret »
Dans le livre de Didier Boursin et Valérie Larose « Pliages et Mathématiques » aux éditions du Kangourou, on trouve un pliage appelé « la boite à secrets ». C’est un joli origami qui peut se faire même avec les plus petits à condition de préparer à l’avance la feuille qui est un triangle équilatéral. Ici on donne une construction de ce triangle à partir d’une feuille a4 et les différentes étapes du pliage:
Origami et exploration spatiale
Parmi les activités de pliage que l’on peut réaliser avec une classe (à partir de la primaire) on peut par exemple, en rapport avec l’exploration spatiale et la nécessité de transporter des panneaux solaires à déployer ensuite dans l’espace, de structures de type « flasher ». Le plus simple de ces flasher a été proposé par Jeremy Shafer :

C’est un exemple d’origami où il va falloir plier d’abord l’ensemble des plis et ensuite manipuler la structure pour la mettre en forme.
La manipulation de cet origami est donnée ici
Une version plus évoluée de cette construction est proposée par la Nasa ! L’origami s’appelle le starshade car il est destiné à cacher la lumière d’une étoile afin d’observer les planètes qui gravitent autour. L’activité se trouve ici
https://www.jpl.nasa.gov/edu/resources/project/space-origami-make-your-own-starshade/
et la feuille à plier ici
Il faut tout de même faire attention et bien s’entraîner avant car le pliage est plus redoutable que celui de Jeremy Shafer.
Jacky Cresson, 2024.