Pendant la Semaine des mathématiques, nous avons proposé quelques défis cryptographiques. Voici les résultats et les solutions !
Quelques liens vers des sites très utiles pour comprendre les techniques cryptographiques :
Mardi 15 mars 2016
Décrypter ce message :
tyenlpyenlqwqyfyklmlqtyhgmjwnkkyjmfogfwgxykywjylkqafyzjnfwgqkuqyly
Félicitations à Nicolas Argaud (Licence mathématiques).
Solution :
Pour décrypter ce message, où les espaces on été supprimés, on pouvait commencer par analyser la fréquence d’apparition des lettres. Cette fréquence est à peu près stable dans un texte écrit dans une langue donnée (sauf si bien sûr on s’applique à rédiger un texte en omettant une certaine lettre ou en choisissant volontairement les mots pour biaiser cette répartition). En français, les statistiques donnent ceci :
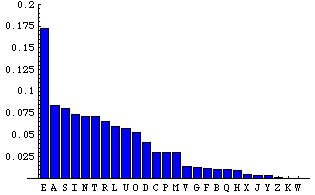
Fréquence des lettres en français. Image extraite du site : http://www.apprendre-en-ligne.net/crypto/stat/francais.html
L’analyse sur ce texte donne (en nombre d’apparitions) :
| Y : 12 | Q, L, K : 6 | W, F : 5 | N, G, J : 4 | M : 3 |
La lettre « y » correspond probablement à un « e ». Ensuite on est bien en peine… le texte est trop court pour que l’analyse statistique puisse bien fonctionner.
On peut remarquer le début du message avec la séquence « tyenlpyenl » qui répète 2 fois un groupe de 4 lettres.
On peut penser à un mot probable dans ce texte, par exemple, « mathematique » ou « mathematicien ». On remarque que ces mots reproduisent la répétition observée : « mathemat » et même « e mathemat« . Il pourrait y avoir correspondance entre « yenl » et « emat ».
Pour le savoir, on substitue ces lettres partout dans le texte. On peut deviner d’autres mots et ainsi trouver des lettres supplémentaires en faisant l’hypothèse « enlpyenlqwqyf » = « mathematicien ». On peut remarquer la fin du message en : « yzjnfwgqkuqyly » qui donne « –anc-i–iete »… ce qui ressemble fortement à un personnage dont il est question pendant cette Semaine des mathématiques : François Viète.
De proche en proche, on trouve le message complet : (en remettant les espaces)
LE MATHEMATICIEN EST UTILE POUR CASSER UN BON CODE SECRET SIGNE FRANCOIS VIETE
Ce cryptage était donc une substitution de lettres : chaque lettre du message initial a été remplacée par une autre lettre.
Mercredi 16 mars 2016
Décrypter ce message :
Félicitations à l’équipe formée de Justine Maniey (L3 mathématiques), Alexandre Sanchez (L3 mathématiques) et Isabelle Greff (maître de conférences département de mathématiques).
Solution :
Ici il s’agit d’un codage et non d’un cryptage : les lettre du message ont simplement été remplacées par des dessins. On peut donc tenter une analyse de la fréquence des symboles pour en déduire les lettres. Mais ce texte est assez court, le résultat est incertain.
Cependant, on peut remarquer que le premier mot est de la forme « ABBC ». Quels mots de 4 lettres peuvent exister avec un doublement de lettre au milieu ? Pas tant que cela… On pouvait penser au prénom « ANNE ».
En analysant la taille des mots, ceux-ci sont assez courts. Ce message pourrait-il être dans une autre langue que le français ? Peut-être… L’anglais a cette particularité d’avoir beaucoup de mots courts. On observe aussi un doublement de lettre dans le dernier mot. Alors quels doublements de lettres peut-on rencontrer en anglais ?
Pour les consonnes, on peut trouver « LL » (bill), « RR » (referred), « TT » (sitting). Pour les voyelles, on peut trouver « OO » (good, mood), « EE » (need, seed…). Ces derniers mots de 4 lettres avec double voyelle pourraient correspondre au premier mot codé.
On peut toujours analyser la fréquence des lettres en anglais, qui se répartie comme suit :
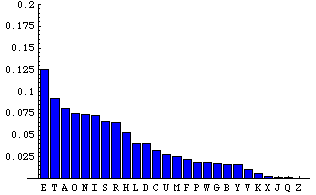
Fréquence des lettres en anglais. Image extraite du site : http://www.apprendre-en-ligne.net/crypto/stat/anglais.html
Le décodage complet conduit à :
NEED EXTRA CASH
MELT DOWN YOUR OLD
UNWANTED HUMANS
WE PAY TOP DOLLAR
Ce texte est en fait tiré de la série télévisée d’animation Futurama, utilisant l’alphabet « alien » donné à ce lien !
Mardi 22 mars 2016
Parviendrez-vous à trouver la clé de cette belle phrase ?
Bfj vr ytprqrtm jra dax w’vbnom cdxbylcstr, geiia vrl f’fvg ltck. Unxd Nnivt
Félicitations à Nelly Barrau, première à avoir trouvé la clé ! (Suivie de près par Nicolas Argaud.)
Ici le cryptage est plus compliqué. Une analyse des fréquences des lettres ne donnera rien, car une même lettre du message original peut être codée en des lettres différentes.
Il s’agit d’un cryptage très classique appelé « chiffre de Vigenère », qui consiste à une utiliser une clé de cryptage, composée de plusieurs lettres. (Avec une clé à une seule lettre, cela revient à appliquer un chiffre de César, c’est-à-dire un simple décalage des n lettres dans l’alphabet.)
Par exemple, la clé était ici TURING. Chaque lettre de la clé correspond à un décalage (A=0, B=1, C=2…) d’un certain nombre de lettres dans l’alphabet.
| T | U | R | I | N | G |
| +19 | +20 | +17 | +8 | +13 | +6 |
On applique ces décalages de façon répétée sur le message original (en ignorant les espaces, les accents et la ponctuation). (Et si on arrive à …W X Y Z, on continue avec A B C D…)
Message : « Ils ne savaient… »
| I | L | S | N | E | S | A | V | A | I | E | N | T | … |
| +19 | +20 | +17 | +8 | +13 | +6 | +19 | +20 | +17 | +8 | +13 | +6 | +19 | +20 |
| B | F | J | V | R | Y | T | P | R | Q | R | T | M | … |
Message codé : « Bfj vr ytprqrtm… »
Ainsi, connaissant la clé, on applique le même procédé sur le message codé, mais en décalant les lettres en sens contraire.
Pour trouver la clé, il existe des astuces. Déjà pour retrouver sa longueur. Il faut observer la répétition de séquences de lettres dans le message codé, que l’on suppose correspondre à des répétitions de séquences de lettres dans le message original. Le nombre de lettres entre ces répétitions de séquences est alors un multiple de la longueur de la clé. Si l’on repère plusieurs répétitions de séquences, alors la longueur de la clé est le plus petit dénominateur commun des nombres de lettres entre les répétitions. Hélas, cette méthode ne fonctionne bien que sur des longs textes.
Une fois la longueur trouvée, on peut écrire le message codé en colonnes et analyser la fréquence des lettres pour chaque colonne (puisqu’une colonne correspond à un décalage de l’alphabet, la fréquence est conservée dans une colonne.)
On peut aussi tester des clés probables 🙂
Pas simple… Néanmoins, le message proposé ici a bien été décodé :
Ils ne savaient pas que c’était impossible, alors ils l’ont fait. Mark Twain
Cryptages : Jacky Cresson. Explications : Clovis Darrigan


