08 | novembre | 2024 | Le Mathematicum

En 1922, Harry Houdini

célèbre magicien, publie un livre intitulé ”Houdini’s paper magic”, qui contient des origamis et des découpages.

L’une des activités présentées s’appelle ”L’étoile à cinq branches” : le but est de découper une étoile à cinq branches dans une feuille de papier carrée en un seul coup de ciseaux ! Plus généralement, si je dessine une forme polygonale sur une feuille, est-il toujours possible de la découper en un seul coup de ciseaux ? La réponse est positive et concerne même toute famille finie de polygones disjoints sur une feuille. C’est le Fold and Cut theorem démontré en 1999 par Erik Demaine, Martin Demaine et Anna Lubiw.

Ce théorème nous a inspiré l’atelier suivant qui peut être réalisé dès l’école primaire.

Pour entrer progressivement dans la complexité que porte ce théorème, nous allons découper en un seul coup de ciseaux plusieurs formes qui chacune vont nous apporter une certaine compréhension de la manière de réaliser le pliage pour une figure polygonale donnée.

L’étoile à 5 branche : le tour de magie de Houdini

On commence par le tout de magie historique de Houdini qui a inspiré ce théorème. On distribue aux participants une étoile à 5 branche et on leur demande de la découper en un seul coup de ciseaux. Attention à imprimer ces dessins sur des feuilles assez légère pour que l’impression de l’étoile puisse se voir en transparence !

Assez rapidement, l’idée de plier le papier va surgir. Ce qui est intéressant ici est de laisser faire les participants car ils ne vont pas forcément formuler un principe qui justifie ce pliage. Leur intuition leur dit de plier mais la raison pour laquelle ils le font n’est la plupart du temps pas explicitée.

Dans la plupart des classes et indépendamment de l’âge, on trouve toujours une personne qui va réussir à découper l’étoile en un seul coup de ciseaux. Une manière de procéder est alors de demander à cette personne de venir expliquer comment elle a procédé.

Voici un pliage possible:

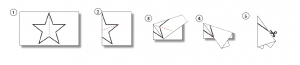
Il faut alors chercher à faire verbaliser la procédure qui a été utilisée et surtout pourquoi avoir plié. À force de discussion, on arrive la plupart du temps à formuler les propositions suivantes:

1- pour arriver à découper la figure en un seul coup de ciseaux il faut faire un pliage qui superpose tous les segments sur un seul.

2- si on a un axe de symétrie dans la figure, cette symétrie permet naturellement de réduire le nombre de segments à découper.

On voit la proposition 2 en action dans l’étape 1 du pliage précédent: on passe de 10 coups de ciseaux dans la figure complète à 5 coups de ciseaux par utilisation d’une symétrie axiale de l’étoile.

Il faut noter que parfois on a seulement une symétrie partielle de la figure comme à l’étape 2.

Une fois compris le but du pliage et ce premier élément pour penser le pliage à faire, on peut aborder une autre figure.

Le rectangle et l’arrivée des bissectrices

On distribue donc des rectangles:

Il faut faire attention à ce que ce rectangle soit « quelconque ». En particulier pas un carré…

En général, tous les participants vont arriver au pliage suivant

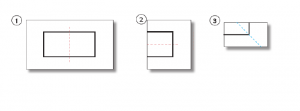
et vont être bloqué par la dernière étape car il n’y a plus de symétries évidentes….

Si personne n’y arrive alors il faut rappeler le principe que nous avons mis en avant pour la construction du pliage: il faut réussir à faire se superposer les segments à découper…donc ramener le petit segment sur le grand…..l’utilisant du pli en diagonale va alors s’imposer rapidement.

On obtient donc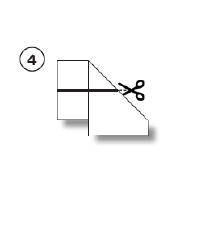Il est bon à ce moment là de regarder plus attentivement ce que l’on a fait et de s’attarder sur ce dernier pli. Il ne provient pas d’une symétrie mais répond à un problème général que nous aurons à gérer pour des figures plus complexes: comment envoyer deux segments qui partent d’un même sommet l’un sur l’autre ?

La réponse est que le pli doit se faire le long de la bissectrice de l’angle formé par les deux segments.

La notion de bissectrice d’un angle est donc un élément essentiel de la construction de notre pliage.

Le triangle et le théorème de Maekawa-Justin

Pour tester cette idée, on essaie de trouver le pliage nécessaire pour découper un triangle quelconque en un seul coup de ciseaux.

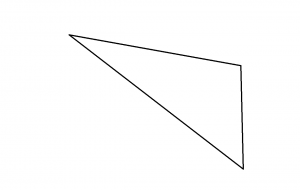
Ce triangle n’a pas de symétries particulières. Nous devons donc nous en remettre à notre seul élément de construction, à savoir les bissectrices de chacun des trois angles du triangle. Je conseille de faire ces plis en plis montagnes de façon à pouvoir chaque fois voir les lignes que l’on superpose.

On va donc avoir les plis suivants:

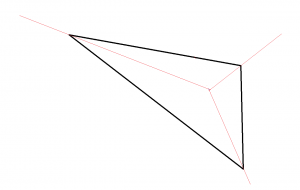
En effectuant les plis, on s’aperçoit rapidement que le pliage ne se met pas à plat et fait une sorte d’étoile à trois branches en 3D.

Certain vont « forcer » le pliage à se mettre à plat et se faisant vont faire apparaître un pli supplémentaire qui est orthogonal à un des côtés du triangle:

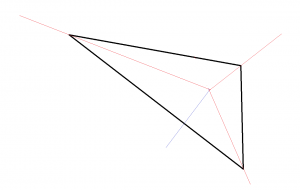
Est-ce que ce pli est nécessaire ? Y-avait-il d’autres façons de procéder ?

En fait, non ! Ce pli supplémentaire est nécessaire par le théorème dit de Maekawa-Justin:

Théorème de Maekawa-Justin: On note M le nombre de plis montagnes et V le nombre de plis vallées en un sommet du canevas d’un pliage qui se met à plat. Alors, on a toujours une différence de 2 entre M et V.

En particulier, en chaque sommet d’un pliage qui se met à plat, on a un nombre pair de plis qui arrivent.

Dans le cas du triangle on avait initialement M=3 (les 3 bissectrices) et V=0 et ce pliage ne pouvait donc pas se mettre à plat. Il était donc nécessaire de rajouter un pli vallée pour satisfaire la condition du théorème. Ce pli est choisi perpendiculaire à un côté quelconque du triangle et passant par l’intersection des 3 bissectrices. Ce faisait, ce pli ramène un segment sur lui même et permet de mettre notre pliage à plat.

Notons au passage que les trois bissectrices se coupent en un point qui est le centre du cercle inscrit au triangle. C’est un joli résultat que l’on peut évoquer en passant suivant le niveau du public.

La fin du voyage…

Nous avons ainsi maintenant plusieurs ingrédients permettant de construire le pliage nécessaire pour une forme donnée afin de la découper en un seul coup de ciseaux. Est-ce que ces éléments permettent de faire facilement toutes les formes possibles ?

Malheureusement, non ! Une illustration des phénomènes possibles est donnée par le pliage nécessaire pour découper un A en un seul coup de ciseaux qui est proposé par Joseph O’Rourke dans son livre How to fold it chez Cambridge University Press
En effet, le pliage est le suivant:

On voit les éléments que nous avons discutés, les bissectrices, les axes de symétries, les plis supplémentaires dus au théorème de Maekawa-Justin, mais aussi l’interaction de ces plis les uns avec les autres. Ces interactions peuvent être compliquées et suivant la manière dont on va rajouter certains plis, le pliage peut devenir vite infernal ! Voici l’exemple du pliage proposé par O’Rourke pour une tortue….

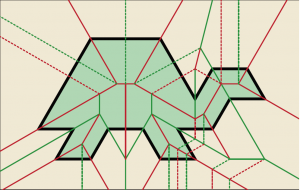
Il y a encore beaucoup de choses à raconter sur la construction de ces pliages mais l’essentiel est là.

Nous n’avons pas traité du découpage simultané de plusieurs formes polygonales. Le but est comme pour les autres de ramener le découpage de chacune à la découpe d’un segment et ensuite de ramener chacun de ces segments l’un sur l’autre. C’est possible mais pas forcément simple ! Pour vous en convaincre, voici le pliage nécessaire pour découper simultanément un rectangle et un carré qui sont bien positionnés l’un par rapport à l’autre !